قطرا متوازي الأضلاع ينصف كل منهما الآخر
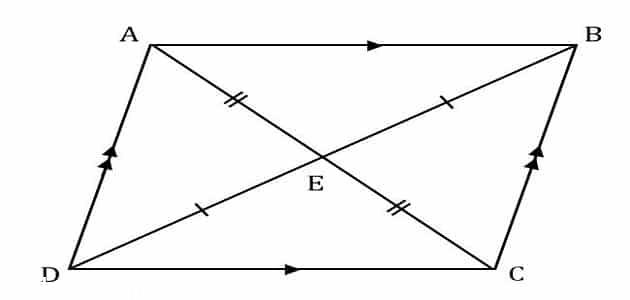
قطرا متوازي الأضلاع ينصف كل منهما الآخر , متوازي الأضلاع هو شكل رباعي له أربعة جوانب ، ولكل جانب ضلعان متقابلان ومتوازيان ومتساويان ، متساويان أيضًا في الطول ، ومتوازى أضلاع متساويان ، والزاوية الكلية 360 درجة ، وسنتناول سؤال مهم في رياضيات المناهج السعودية ، يتساءل الكثير من الطلاب عن إجابته ، وهذا السؤال يدور حول قطر متوازي منصف لبعضنا البعض ، سنتناول الإجابة على هذا السؤال من خلال الأسطر التالية فابق معنا. مع سلسلة من الحلول النموذجية التي يقدمها موقع الفهرس.
قطرا متوازي الأضلاع ينصف كل منهما الآخر
تتضمن الإجابة على هذا السؤال تحديد محتوى مصطلح “متوازي الأضلاع” المنصف لبعضه البعض ، سواء أكان صحيحًا أم خاطئًا ، والإجابة الصحيحة عليه كالآتي:
العبارة صحيحة.
خصائص متوازي الاضلاع
هناك العديد من الخصائص التي تميز الهندسة المتوازية الجوانب ، منها:
بالتوازي ، كل ضلع معاكس بالتساوي.
في متوازي الأضلاع ، مساحته ضعف حجم المثلث المكون من جانبين وقطر.
في متوازي الأضلاع ، كل قطر عادل للآخر.
في متوازي الأضلاع ، يتقاطع القطر عند نقطة تشكل مركز متوازي الأضلاع ، والمعروفة باسم مركز متوازي الأضلاع.
في متوازي الأضلاع ، يتم تقسيم أي ممرات مستقيمة عبره إلى شكلين متطابقين.
في متوازي الأضلاع ، كل زاوية من الزاويتين المتقابلتين متساويتان.
بالتوازي ، مجموع مربعات أطوال الأضلاع يساوي مجموع القطرين ، المعروفين باسم متوازي الأضلاع.
في متوازي الأضلاع ، مجموع كل من الزاويتين المتحالفين يساوي 180 درجة.
حالات خاصة من متوازي الأضلاع
هناك عدة حالات للهندسة متوازية الجوانب خاصة بها دون أشكال هندسية أخرى ، وهذه الحالات هي كما يلي:
إذا كان متوازي الأضلاع متعامدًا ، أو كانت أطوال الأضلاع المجاورة متساوية في هذا المتوازي ، يصبح الشكل معطى.
إذا تساوى قطر متوازي الأضلاع أو إحدى زواياه ، يصبح الشكل مستطيلاً.
إذا كان متوازي الأضلاع مستطيلًا ومحددًا معًا ، يصبح الشكل مربعًا.
في الإجابة على سؤال الرياضيات في المنهاج السعودي للفصل الدراسي الثاني والذي يتعامل مع متوازي أضلاع عادل لبعضه البعض ، فإن متوازي الأضلاع يرتبط بقياس المحاور والأقطار والزوايا بأشكال مختلفة ، وحديثنا عن الخصائص متوازيات الأضلاع ، وحالات خاصة من متوازي الأضلاع ، وصلنا إلى نهاية هذا المقال ، ونأمل أن ينال مقالنا التعليمي إعجابكم والاستفادة الكاملة.
